Posted by : Citrapurnama28
Rabu, 25 Februari 2015
mungkin ada yang masih ga tau apa itu bilangan fibonacci? emang rada sedikit aneh sih kalo baru pertama kali denger soalnya kita taunya cuma bilangan bulat kalo nggak bilangan cacah, nih sekarang aku mau ngasih tau apa sih sebenernya bilangan fibonacci itu.
Bilangan Fibonacci
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
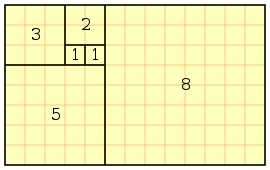
Dalam matematika, bilangan Fibonacci adalah barisan yang didefinisikan secara rekursif sebagai berikut:- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...
- Fn = (x1n – x2n)/ sqrt(5)
- Fn adalah bilangan Fibonacci ke-n
- x1 dan x2 adalah penyelesaian persamaan x2 – x – 1 = 0.
Asal mula
Berdasarkan buku The Art of Computer Programming karya Donald E. Knuth, barisan ini pertama kali dijelaskan oleh matematikawan India, Gopala dan Hemachandra pada tahun 1150, ketika menyelidiki berbagai kemungkinan untuk memasukkan barang-barang ke dalam kantong. Di dunia barat, barisan ini pertama kali dipelajari oleh Leonardo da Pisa, yang juga dikenal sebagai Fibonacci (sekitar 1200), ketika membahas pertumbuhan ideal dari populasi kelinci.Gimana udah pada paham belum? gampangkan ternyata bilangan fibonacci itu angka berikutnya tinggal ditambah-tambahin aja