はじめまして!!

Persamaan Garis Lurus; Fungsi, Persamaan, dan Pertidaksamaan Kuadrat

Persamaan Garis Lurus

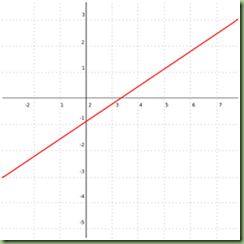
Bentuk umum

m disebut gradien / kemiringan

Persamaan garis lurus yang melalui titik (x₁ , y₁) dan (x₂, y₂) adalah

cat.
Persamaan garis lurus adalah suatu fungsi dengan f(x) = y.

Fungsi Kuadrat

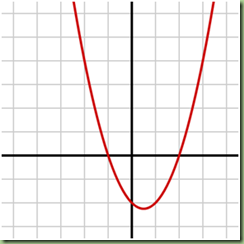
Bentuk umum


Persamaan Kuadrat

Cara penyelesaiannya :

• Rumus ABC

Diskriminan

Jika D>0 maka x₁ dan x₂ berbeda, x₁, x₂ bilangan real (Secara geometri, kurva f(x) memotong sumbu x)
Jika D=0 maka x₁ dan x₂ sama, x₁, x₂ bilangan real (Secara geometri, kurva f(x) bersinggungan dengan sumbu x)
Jika D<0 maka x₁ dan x₂ bilangan kompleks (Secara geometri, kurva f(x) tidak memotong maupun bersinggungan dengan sumbu x)

• Bentuk  x² + bx + c = 0

Cari bilangan bulat p dan q sedemikian sehingga  p . q = c dan p + q = b, maka
x² + bx + c = 0
(x + p) (x + q) = 0
x₁ = – p dan x₂ = –q

• Bentuk  ax² + bx + c = 0

Cari bilangan bulat p dan q sedemikian sehingga  p . q = a . c dan p + q = b, maka
ax² + bx + c = 0
ax² + px + qx + c = 0    atau    ax² + qx + px + c = 0
(ax² + px) + (qx + c )= 0    atau    (ax² + qx) + (px + c )= 0
faktorkan setiap grupnya sedemikian hingga
(nx + m) (rx + s) = 0
x₁ = – m / n dan x₂ = –s / r
Contoh-contoh

1. x² + 3x + 2 = 0

b = 3 dan c = 2
p = 1 dan q = 2 karena 1 + 2 = 3 dan 1 . 2 = 2, maka
x² + 3x + 2 = 0
(x + 1) (x + 2) = 0
x₁ = – 1 dan x₂ = –2
Himpunan penyelesaian = { –1 , –2 }
2.  2x² + 7x + 3 = 0
a = 2, b = 5, c = 3
a . c = 6
p = 1 dan q = 6 karena 1 . 6 = 6 dan 1 + 6 = 7, maka
2x² + 7x + 3 = 0
2x² + x + 6x + 3 = 0
(2x² + x) + (6x + 3) = 0
faktorkan :
(2x² + x) = x (2x + 1)
(6x + 3) = 2 (2x + 1) , maka
(x + 2) (2x + 1) = 0
x₁ = – 2 dan x₂ = –1 / 2
Himpunan penyelesaian = { –2 , –1 / 2 }
Pertidaksamaan Kuadrat
Bentuk persamaan

= diganti dengan <, >, <, atau >.
Cara penyelesaian
Rubah pertidaksaan tersebut menjadi suatu persamaan
Selesaikan persamaan tersebut
Uji tanda
Contoh
x² + 3x + 2 > 0
Pertidaksamaan tersebut dirubah menjadi persamaan:
x² + 3x + 2 = 0 kemudian cari x
dari contoh sebelumnya diperoleh  x₁ = – 1 dan x₂ = –2
Uji tanda :

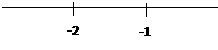
ambil sebuah bilangan real yang terletak sebelum – 2, diantara –2 dengan –1, dan setelah –1 :
misal –3 , –3/2, 0
masukkan tiga bilangan tersebut ke f(x) = x² + 3x + 2
f(-3) = 2  tanda +
f(-3/2) = –1/4  tanda –
f(0) = 2 tanda +
maka

karena x² + 3x + 2 > 0 maka daerah penyelesaiannya adalah yang bertanda + dan –1, –2 tidak termasuk

maka himpunan penyelesaiannya adalah { x<-2 atau x>-1 } atau dengan notasi interval